Flattening a Tapered Elliptical Part
An elliptical desk meets a brick wall, and software wizards get their heads around a very tricky dimensional problem. October 1, 2005
Question
I work for a custom cabinet shop and recently ran into a problem. We are constructing an elliptical reception desk (approximately 10 1/2' long). The desk is a little more than half of the ellipse. The problem is, the wall is on a nine degree taper. I have the entire desk drawn to cut out on the CNC. I need to figure out how to flatten the 3-D image of the wall panel so I can cut it out. Any other suggestions or methods will be greatly appreciated.
Forum Responses
(CAD Forum)
From contributor A:
Did you check out the thread here recently on this subject?
From the original questioner:
Yes I did take a look at that thread, but it seems most of that software is for radius not ellipse. I have downloaded several software layouts, but no luck with the ellipse yet.
From contributor M:
What software are you using?
From contributor P:
As far as I know there is no program that will flatten a tapered elliptical part. It gets tricky because an ellipse has a moving center, and there is stretching and compressing involved.
There may be a better way to do it, but I would just draw the ellipse for the top and the bottom and divide the circumferences and cut out sections and let them run long. Smooth the wall with a circular sander (boat builder trick). Then cut the veneer in sections and use veneer tape and a vacuum bag.
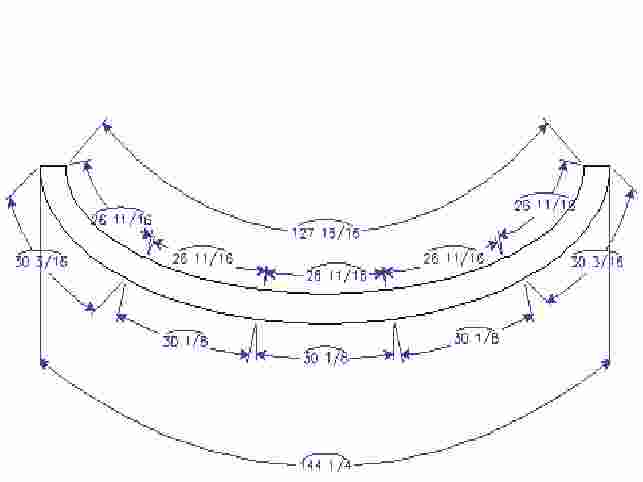
Click here for full size image
From the original questioner:
I am using a demo version of AutoCad 2005, but mostly R14 also enroute 3 for the cnc. Thanks Contributor P - I have already thought of that for my last resort, but I really want to cut it in one piece. We have just got a CNC and would like to use it.
From contributor R:
I have to do a lot with elliptical stairs and the only realistic solution is to convert the ellipse to multiple arc segments. Obviously, this is mostly because offsets of ellipses become nearly intangible geometry (basically spline curves). Usually, a 3-arc quadrant makes a very good representation. I have a template in Solidworks that uses an ellipse to act as a raceway on which 3 tangent arcs ride and conform to produce a quadrant. Then, in Solidworks, I generate my parts as sheet metal, which I then fold to the required shape.
